refaaxis.blogg.se - Sss similarity

#Sss similarity full#

AAS(Angle-Angle-Side): Where two angles of any two triangles along with a side that is not included in between the angles, are equal to each other. Two geometric figures are similar if one is a scaled version of the other.ASA(Angle-Side-Angle): Where two angles along with a side included in between the angles of any two triangles are equal to each other.SAS(Side-Angle-Side): Where two sides and an angle included in between the sides of two triangles are equal to each other.

SSS(Side-Side-Side): Where three sides of two triangles are equal to each other.

You could not only going similar to ebook gathering or library or. The 4 different triangle congruence theorems are: This is an applet for you to investigate why SSS Similarity is valid and answer the following questions. Getting the books 7 3 Triangle Similarity Aa Sss Sas now is not type of challenging means. The rule helps in proving if the triangles are congruent or not. The SSS rule states that, if three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent. The three triangle similarity theorems are: At the same time a person 6 ft tall casts to this real world problem. Click on the file below to see the picture. SSS Similarity If the corresponding side lengths of two triangles are proportional, then the triangles are similar In sunlight, a cactus casts a 9-ft shadow. What are the Three Triangle Similarity Theorems? Triangle Proportionality Theorem and Converse.

In the SSS postulate, all three sides of one triangle are equal to the three corresponding sides of another triangle. Side-Side-Side (SSS) Similarity Theorem: If the lengths of the corresponding sides of two triangles are roportional, then the triangles must be similar.

In the SAS postulate, two sides and the angle between them in a triangle are equal to the corresponding two sides and the angle between them in another triangle.

#Sss similarity full#

SAS full form is "side-angle-side" and SSS full form is "side-side-side." Let's use these steps and definitions to practice using the SSS Similarity Theorem to find missing side lengths in similar triangles with the following two examples. What is the Difference Between SAS and SSS?īoth SAS and SSS rules are the triangle congruence rules.

SSS similarly can be proved by showing that the side lengths of one triangle are proportional to the side length of the other triangle. Under the SSS theorem, if all the three sides of one triangle are equal to the three corresponding sides of another triangle, the two triangles are congruent. SSS Criterion stands for side side side congruence postulate. We can represent this in a mathematical form using the congruent triangles symbol (≅). This (SSS) is one of the three ways to test that two triangles are similar. Since these two triangles are of the same size and shape, we can say that they are congruent. Triangle Similarity Test - SSS Three sides in proportion Definition: Triangles are similar if all three sides in one triangle are in the same proportion to the corresponding sides in the other. SSS similarity : If the corresponding sides of two triangles are proportional, then the two triangles are similar. Hence, it indicates that the corresponding parts of congruent triangles are equal. This means that AB falls on XY, BC falls on XZ, and AC falls on ZY. For example, the two triangles above are said to be congruent according to the SSS congruence rule. Congruence is the term used to describe the relation of two figures that are congruent. The word congruent means equal in every aspect or figure in terms of shape and size. Look at the triangles below, the triangles are said to be congruent because AC = ZY, CB = ZX, and AB = XY. This essentially means that any such pair of triangles will be equiangular i.e.

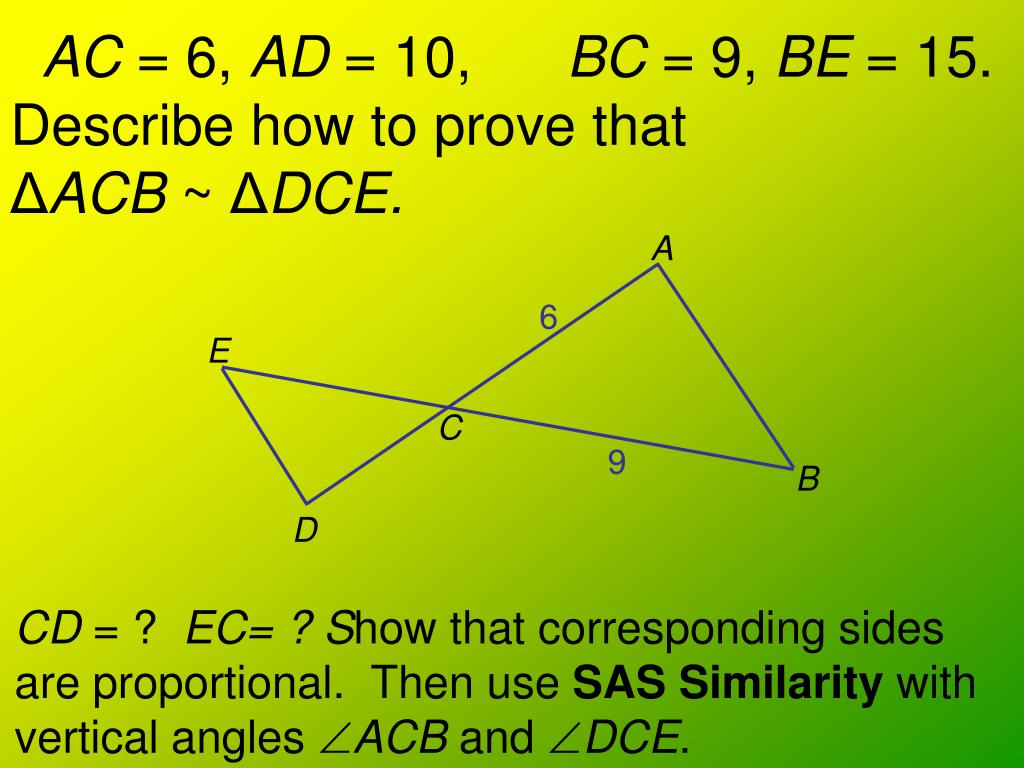
Under this criterion, if all the three sides of one triangle are equal to the three corresponding sides of another triangle, the two triangles are said to be congruent. Hence, $\triangle ABC\cong\triangle DPQ$ by SSS rule.SSS Criterion stands for Side-Side-Side congruence postulate. Let there be two triangles $\triangle ABC$ and $\triangle DEF$, such that: Since the two triangles have two corresponding congruent angles, they are similar.